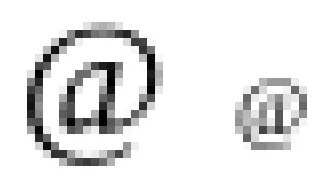Pixel? dpi? Was hat das mit Thunderbird zu tun?
Wie viele andere Anwendungen auch, hat Thunderbird u. a. die Aufgabe, Inhalte auf dem Bildschirm darzustellen. Schaut man sich hier im Forum diverse Screenshots an und liest die Hilferufe über viel zu kleine Schrift, wird klar, daß es da einiges zu verbessern gibt. Sicher läßt sich vieles durch die richtige Auswahl der Schriftart/-größe[6] erreichen, für eine optimale Einstellung sollte man sich aber etwas näher mit den Grundlagen beschäftigen. Ich hoffe, dieser Artikel kann dazu beitragen.
Zur Einstimmung möge folgendes Testbild dienen, ein Gittermuster mit einer Strichbreite von nur einem Bildpunkt. Wer mag, kann sich das Bild in verschieden Verkleinerungsmaßstäben ansehen und wird wahrscheinlich von dem Ergebnis überrascht sein …
Ein modernes Bildschirm enthält eine Matrix von ansteuerbaren Bildpunkten. Um es nicht zu kompliziert zu machen, beziehe ich mich auf einen LCD-Bildschirm und fasse die RGB-Punkte zu einem Bildpunkt (Pixel) zusammen. Die Anzahl der Bildpunkte horizontal und vertikal wird als native Auflösung des Bildschirms angegeben.
Sie ist nicht abhängig von den geometrischen Ausmaßen des Bildschirms: Ein Bildschirm mit einer Diagonalen von 150 cm mit einer Full HD Auflösung enthält 1920 Bildpunkte horizontal und 1080 Bildpunkte vertikal - ein Smartphone mit einer Diagonalen von 15 cm und der gleichen Auflösung enthält die gleiche Anzahl Bildpunkte!
Statt cm/mm wird bei Bildschirmen oft auch die Maßeinheit Zoll (inch) verwendet. Hier eine Aufstellung der wichtigsten Einheiten und ihre Festlegung:[box]
1 Zoll[1] (inch) = 25,4 mm
1 DTP-Punkt[2] (pt) = 1 inch ÷ 72 = 0,352777778 mm
12 pt = 12 × 0,352777778 mm = 4,233333336 mm
Für CSS[3] ist festgelegt:
1 Pixel (px) = 1 inch ÷ 96 = 0,264583333 mm[/box]
Die Punktdichte[4] gibt die Anzahl von Bildpunkten pro Längeneinheit an.
Gebräuchlich sind die Einheiten: dpi (dots per inch) und ppi[5] (pixel per inch)
Wofür ist die Punktdichte (dpi) nun gut?
Gegeben sei ein Netbook mit einer Diagonalen von 255 mm bei einer nativen Auflösung von 1024 × 600 Bildpunkten. Die Breite des sichtbaren Bildschirms beträgt 220 mm, die Höhe 129 mm.
Daraus läßt sich jetzt die Punktdichte (dpi) berechnen:
[box]
Punktdichte (in dpi) = Anzahl Bildpunkte × 25,4 ÷ Länge (in mm)[/box]
Auflösung horizontal = 1024 × 25,4 ÷ 220 mm = 118 dpi
Auflösung vertikal = 600 × 25,4 ÷ 129 mm = 118 dpi
Ein weiteres Beispiel: ein Monitor mit einer Diagonalen von 547 mm bei einer nativen Auflösung von 1920 × 1080 Bildpunkten (Full HD). Die Breite des sichtbaren Bildschirms beträgt 477 mm, die Höhe 268 mm.
Auflösung horizontal = 1920 × 25,4 ÷ 477 mm = 102 dpi
Auflösung vertikal = 1080 × 25,4 ÷ 268 mm = 102 dpi
Wie man sieht, ist in beiden Fällen die Punktdichte horizontal und vertikal gleich; das muß aber nicht immer so sein.
Jetzt stellt sich die Frage: Welches Bildschirm liefert die besseren Bilder - das kleine Netbook oder der Full HD Bildschirm?
Die Antwort ist abhängig vom Betrachtungsabstand: bei gleichem Abstand liefert das Netbook die besseren Bilder (größere Punktdichte = mehr Bildpunkte pro Längeneinheit = mehr Einzelheiten sind für eine gegebene Fläche darstellbar)!
Laut BGI 650 (Leitfaden für die Gestaltung von Bildschirm- und Büroarbeitsplätze) sollte für ein ermüdungsfreies Arbeiten die Zeichenhöhe von Großbuchstaben (ohne Ober-/Unterlängen) so gewählt werden, daß sie unter einem Sehwinkel von mindestens 22 Bogenminuten erscheinen.
Was mit Ober- und Unterlängen gemeint ist, zeigt das folgende Bild:
Als Faustformel für die Berechnung der minimalen Zeichenhöhe gilt:
[box]
Minimale Zeichenhöhe (mm) = Betrachtungsabstand (mm) ÷ 155[/box]
Die notwendige, minimale Zeichenhöhe wächst also linear mit dem Betrachtungsabstand:
500 mm ÷ 155 = 3,225806452 mm
600 mm ÷ 155 = 3,870967742 mm
700 mm ÷ 155 = 4,516129032 mm
800 mm ÷ 155 = 5,161290323 mm
Jetzt könnte man auf die Idee kommen und sagen: eine 12 pt große Schrift (= 4,233333336 mm) ist mehr als ausreichend für einen Betrachtungsabstand von 500 mm. Stimmt leider nicht! Wir erinnern uns an die Ober-/Unterlängen - die 12 pt gelten für den gesamten Bereich, in dem ein Zeichen dargestellt wird.
Wie soll man 3,225806452 mm auf dem Bildschirm denn nun ausmessen? Dazu ein kleiner Trick: man schreibt in einem Textverarbeitungsprogramm ein «E» mit der Schriftgröße 200 und mißt die Höhe aus, auf meinem Bildschirm sind das in der von mir gewählten Schriftart 48,5 mm. Damit ergibt sich für eine Schriftgröße von 1 pt: 48,5 mm ÷ 200 = 0,2425 mm Zeichenhöhe.
Eine Schriftgröße von 12 pt ergibt also:
[box]
48,5 mm ÷ 200 × 12 = 2,91 mm (Zeichenhöhe Buchstabe 'E')[/box]
Das entspricht eindeutig nicht den o. g. Anforderungen! Erst eine Schriftgröße von 13 pt ergibt 3,1525 mm Zeichenhöhe auf meinem Netbook; damit kann ich gut leben.
Es kommt aber noch ein weiteres Kriterium hinzu - die Schriftart. Einige Schriftarten erscheinen unterschiedlich groß bei gleicher Schriftgröße (in pt), das betrifft auch den Unterschied zwischen gleichen Schriftarten mit und ohne Serifen.
Hier ein Beispiel mit der Schriftart «Liberation serif» vs. «Liberation sans» gleicher Größe:
Die minimale Schriftgröße ist also vom Betrachtungsabstand und von der gewählten Schriftart abhängig!
Welche Rolle spielt nun der dpi-Wert (die Punktdichte)? Je höher der dpi-Wert ist, umso mehr Feinheiten können bei einer vorgegebenen Fläche dargestellt werden.
Ein Beispiel mit dem Zeichen «@» soll das verdeutlichen, das folgende Bild enthält die Darstellung in der Schriftgröße 96, 48, 24, 12 und 6 pt.
Soweit sieht das ja nicht schlecht aus. Das Problem bei kleinen Schriftarten wird aber sofort deutlich, wenn man dasselbe Bild um den Faktor 2, 4 oder 8 vergößert (das größte Zeichen fällt dabei raus):
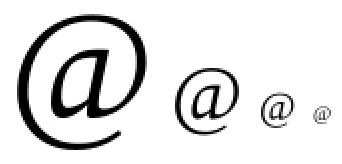
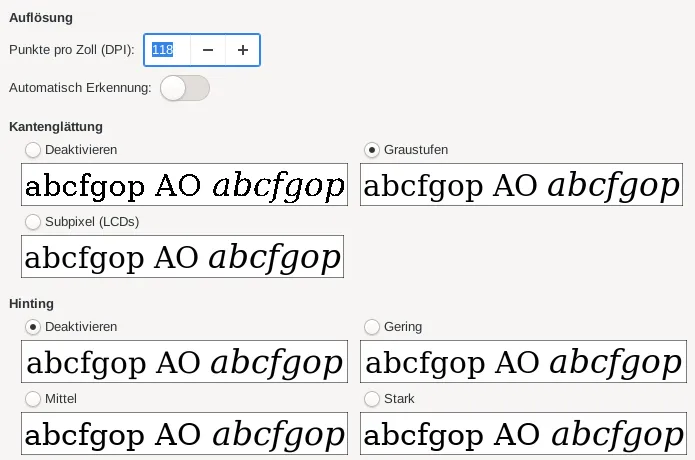
Wie man sieht, stehen bei kleinen Schriftarten für die Rundungen nicht genügend Bildpunkte zu Verfügung, um diese sauber darzustellen. Um das Ausfransen der Zeichenränder bei zu wenig Bildpunkten zu mindern, greift das System zu einem Trick: Kantenglättung. Auf meinem System sieht das so aus:
Man kann auch Kantenglättung mit Subpixeln einstellen, was zwar feinere Abstufungen erlaubt, unter Umständen aber unschöne Farbsäume erzeugt. Daher habe ich auf meinem System (Linux) Kantenglättung mit Graustufen eingestellt.
Was passiert nun, wenn man Bilder auf dem Bildschirm beliebig vergrößert oder verkleinert? Dazu wieder einige Beispiele mit einem Schachbrettmuster von 1, 2, 4 und 8 Bildpunkten:
Solange die Vergrößerungen ganzzahlig sind, ist das kein Problem; die Anzahl der Bildpunkte horizontal und vertikal wird einfach vervielfacht. Mit beliebiger Vergrößerung ergeben sich allerdings interessante Effekte, besonders bei dem 1×1 Schachbrettmuster. (Die Bilder sind extra im bmp-Format angefertigt, um Auswirkungen durch die Kompression auszuschließen.)
Das folgende Beispiel zeigt das auf 37 % verkleinerte 8×8 Schachprettmuster. Wieder ergeben sich merkwürdige, nicht vorhersagbare Effekte. Das liegt einfach daran, daß Bildpunkte nicht beliebig verkleinert werden können, sondern auf dem Raster des Bildschirms abgebildet werden müssen. Der Algorithmus, mit dem das System diese Anpassung vornimmt, ist sicher bei jedem System unterschiedlich.
Was bei einem «normalen» Bild vielleicht gar nicht auffällt, stört bei geometrischen Mustern doch erheblich. Jetzt wird vielleicht auch verständlich, wie die Effekte bei dem Eingangsbild (Gittermuster) zustandekommen. Ein «intelligenter» Algorithmus würde beim Verkleinern die Linien unangetastet lassen und nur die Zwischenräume verkleinern. So weit sind wir heute aber noch nicht …
Was ich mit all dem zeigen wollte, ist: Man sollte sich nicht auf die Default-Einstellungen des Systems verlassen, sondern für die eigenen Anforderungen anpassen. Das betrifft vor allem die richtigen dpi-Werte, die für eine optimale Darstellung wichtig sind. Im Idealfall ist die Zeichenhöhe für eine gegebene Zeichengröße auf jedem Bildschirm gleich - egal wie groß der Bildschirm auch ist!
Windows z. B. verwendet m. W. nach wie vor den Wert 96 dpi als Grundlage für die Bildschirmdarstellung. Dieser Wert passte früher mal für uralte Monitore mit einem Seitenverhältnis von 4:3 und einer Diagonale von 13,4 inch, für einen modernen Bildschirm mit dem Seitenverhältnis von 16:9 müßte die Diagonale 23 inch betragen.
Auf meinem Linux-Rechner kann ich mir die Werte des Systems direkt anzeigen lassen:
xdpyinfo | grep -C1 dimensions
screen #0:
dimensions: 1024x600 pixels (220x129 millimeters)
resolution: 118x118 dots per inch
Wie das unter anderen Betriebsystemen möglich ist, weiß ich leider nicht. Hier müßte man evtl. den Bildschirm ausmessen, den korrekten dpi-Wert nach der o. g. Formel berechnen und den Skalierungsfaktor (unter Windows) anpassen. Vielleicht hat ein anderer Anwender dazu mehr Informationen …
Um das optimale Ergebnis für den eigenen Arbeitsplatz zu erreichen, sind also folgende Schritte erforderlich:
- Helligkeit, Kontrast und Farbsättigung des Bildschirms korrekt einstellen[7]
- Auflösung der Grafikkarte auf die native Auflösung des Bildschirms einstellen
- korrekten dpi-Wert ermitteln und im System einstellen
- Eine passende Schriftart und Schriftgröße anhand der o. g. Kriterien wählen[6]
Viel Erfolg!
P. S. Wer Fehler findet, darf sie gerne behalten oder hier mitteilen.
[1] https://de.wikipedia.org/wiki/Zoll_(Ein…che_Ger%C3%A4te
[2] https://de.wikipedia.org/wiki/Schriftgrad#DTP-Punkt
[3] https://de.wikipedia.org/wiki/Cascading_Style_Sheets
[4] https://de.wikipedia.org/wiki/Punktdichte
[5] https://en.wikipedia.org/wiki/Dots_per_…r_DPI_standards
[6] Thunderbird 78 und die Schriftarten/-größen
[7] https://www.burosch.de/tv-bildeinstellungen/testbilder.html